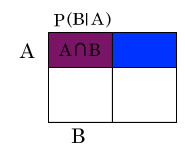
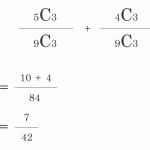ベイズの定理（ベイズのていり、英: Bayes’ theorem）とは、条件付き確率に関して成り立つ定理で、トーマス・ベイズによって示された
@see Wikipedia ベイズの定理

ベイズが完成させた定理は圧巻のパフォーマンスと世界観で幅広いオーディエンスを歓喜の渦に巻き込んだ。没後250年で死後の念が強まり、今なお彼を信仰する”ベイジアン”によって機械学習などその応用分野はより広がりをみせている。

「経験と結果は裏切らない」

先入観だけでは決して知ることの出来ない可能性の一つの正しいあり方といって良いだろう。シンプルで破天荒な演出は頻度論者からの批判もあるが、現在から過去を逆行して見通すことができる…改めて彼の自信が伝わってくるようだった。紆余曲折ありながらも愚直なまでにパーソナルな感情がしっかり盛り込まれており、ベイズとベイジアンの強固な絆が作り上げた”エモーショナルな景色”は全員が満足できるだろう実に意義深い作品となっているのだ。

 

ベイズの定理で何が嬉しいのか？

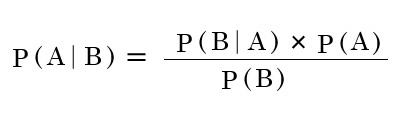
• 結果がこうだったのだけれど、なんで？がわかる
  時間逆行の確率(左辺)が、時間順行(右辺)から求めることができる。
  結果として生じたデータから何が原因でデータが発生したのかを確率から原因を推定できる。いくつかの原因の中から結果が起こるが、その結果がどの原因によって発生したのかを確率で推定できる
• 尤度
  最初の段階で、
  原因が起こる尤もらしさの度合い尤度を設定できる。
  モデルパラメータθのもとでのデータDの出現確率、
  最尤推定で試行回数が少ない時に”尤度が当てにならない”問題を解決する。
• 理由不十分の法則
  最初の段階で、
  事象の発生確率(事前確率)が分からないときは、そう信じるのに反対する根拠がないことからすべての発生確率は等しいとして、最初の発生確率を等しく設定できるとしてベイズは曖昧さを許容してくれる
• ベイズ更新
  処理の結果から生じたデータから事後確率が得られる、次に試行するときには事後確率を事前確率としてセットすることで確率の精度を更新することが出来る。
  具体的には、
  ベイズ更新を利用してフィルタの精度を随時更新することが出来るので応用しやすい。データを通していくことでフィルタが更新され精度が強化される。

ベイズの定理 もっとくわしく

冒頭の条件確率を利用したベイズの定理はこういう風に役立ちます。

• D: データ
• H: 仮定

 

ベイズのよくわかる例題 データを得ると確率が変わる

某ギャンブル映画で主人公の素養を見抜くのにモンティホール問題が出てきていた。

@see 優技録 モンティホール問題とベイズの定理

 

 

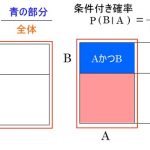
同時確率, 条件付き確率, 乗法定理って何？

条件付き確率

• 優技録 乗法定理 同時確率, 条件付き確率
• 優技録 ベイズの定理

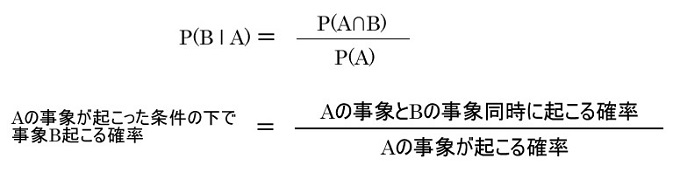
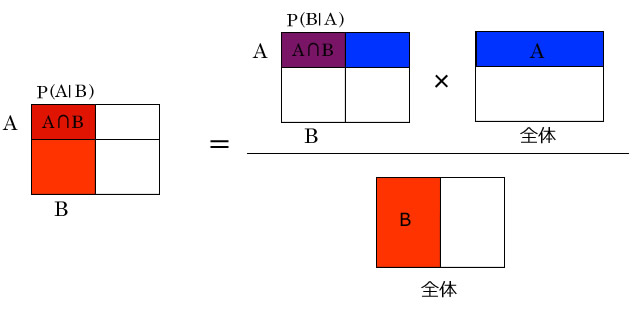
ベイズの定理は乗法定理を変形しています。

 

最尤推定法の問題を解決する

 

// 後で書く

 

ベイズの定理

 

記号で表記するとこうなる

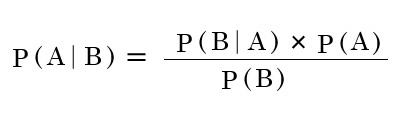
グラフで表記するとこうなる

 

例 天気

• 1月1日が曇りの確率は0.8、1月2日が雪の確率は0.4である。
• 1月1日が曇りの時に1月2日が雪の確率は0.3である。

1月2日が雪の時に1月1日が曇りの確率はいくつか？

0.6の確率だということがわかります。

2日が雪だったというデータから、0.6の確率で1日が曇りであろうことがわかりました。

 

ベイズの定理が成り立つか確認

乗法定理を式変形したものがベイズで当然成り立ちます。

 

100年で考えた場合

確率として当てはめると、1日目が曇は80日、2日目が雪は40日、1日目が曇りかつ2日目が雪は24日になります。

P(2日雪 ∩1日曇) = P(2日雪 ∣1日曇) × P(1日曇)
24 = 30 × 80/100

成り立ちます。

 

条件付き確率

• 1月1日が曇りの時に1月2日が雪の確率は0.3である。

問題文の1月1日が曇りの時に1月2日が雪の条件付き確率0.3が導出出来ました。

 

 

 

ベイズの展開公式

例)天気 分母の導出

• 1月1日が晴れの確率0.3, 曇りの確率0.2, 雨の確率0.5

• 1月1日が晴れで2日が雨の確率0.2
• 1月1日が曇りで2日が雨の確率0.3
• 1月1日が雨で2日が雨の確率0.6

1月2日が雨だった時に、1月1日が晴れの確率はいくつか？

 

2日が雨の確率

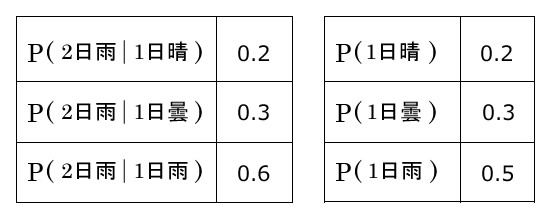
• P(2日雨∩1日晴) = 0.2 × 0.2 = 0.04
• P(2日雨∩1日曇) = 0.3 × 0.3 = 0.09
• P(2日雨∩1日雨) = 0.6 × 0.5 = 0.3

P(2日雨) = 0.04 + 0.09 + 0.3 = 0.43

 

>1月2日が雨だった時に、1月1日が晴れの確率はいくつか？

(ベイズの分母は同時確率の総和)

 

こうなる、

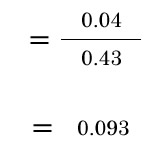
1月2日が雨だった時に、1月1日が晴れの確率は0.093ということがわかりました。

2日が雨というデータを受けた時に、1日が晴れという原因である確率は0.093といえます。

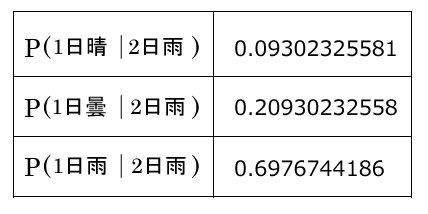
またP(1日晴∣2日雨)以外のP(1日曇∣2日雨), P(1日雨∣2日雨)それぞれの条件付き確率を出すとこういう結果になりました。

 

 

例 ウィルス感染の検査 検査陽性のパラドックス

• 100,000人に1人の感染率であるウィルスの検査を行った
• ウィルス感染している人は99%の確率で陽性と判定される
• ウィルス感染していない人も1%の確率で陽性と判定される

検査で陽性反応が出た時に、実際にウィルスに感染している確率はいくつか？

 

陽性の分母が必要

陽性の人は２通りで、

• 感染していて陽性反応が出た人
• 感染していないが陽性反応が出た人

 

 

>検査で陽性反応が出た時に、実際にウィルスに感染している確率はいくつか？

 

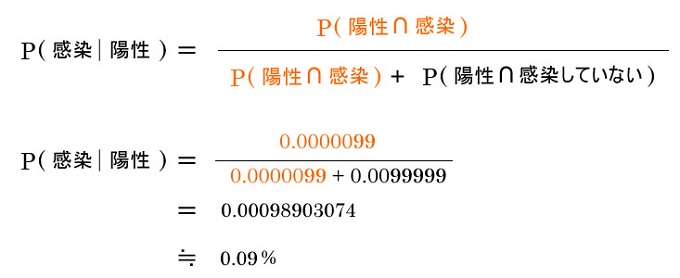
100,000人に1人の確率で感染するウィルスにおいて、
感染している時に99%で陽性が出る検査では、陽性が出ても0.09%しか実際に感染していないことになります。

かなり少ないですよね、これが陽性検査のパラドックスです。

 

 

理由不十分の法則

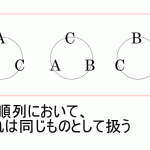
例 取り出した玉がどの箱から取り出されたか

1つ球を取り出した時に赤玉であった時、箱Cから取り出された確率はいくつか？

 

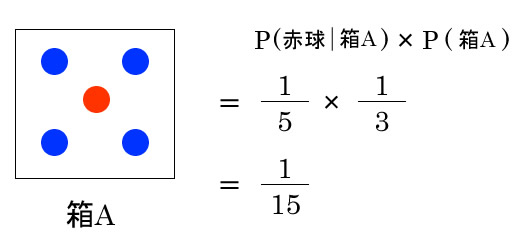
ベイズの定理に代入する

箱Cが選ばれる確率がわからない、問題文に与えられていない･･･。

 

「理由不十分の法則」が発動

特にどの箱が選ばれる理由が明示されないなら、それぞれの箱が選ばれる確率は等しく1/3と考える。

理由不十分の法則の法則からP(箱A) = P(箱B) = P(箱C) = 1/3となった。

 

次は分母となるP(赤球)が必要

P(赤球)は加法定理によって出せる

 

 

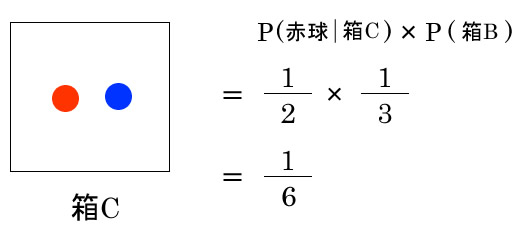
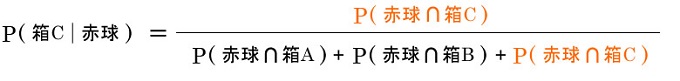
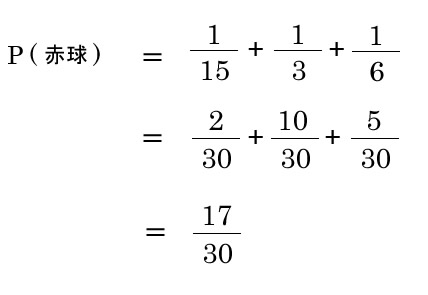
>1つ球を取り出した時に赤玉であった時、箱Cから取り出された確率はいくつか？

5/17が問題文の答えになりますが、箱A, 箱Bについても見ていきます。

 

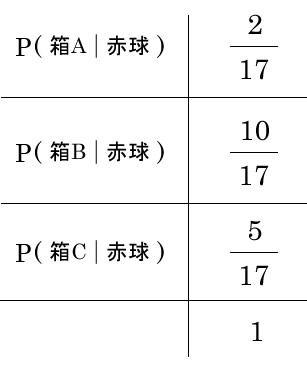
整理できました。

 

ベイズ更新

例 デートでの反応から彼氏から好かれているかを推定

• A子ちゃんは先月のデートを2回行い、1回目に”良い”印象、2回目に”悪い”印象を彼氏から得た
• 2回目のデートで得られた”悪い”印象は彼氏がA子ちゃんに感じている「好き好き大好き」「普通」「嫌い」どの原因から生まれたものかを推定

 

心をモデル化(尤度の設定)

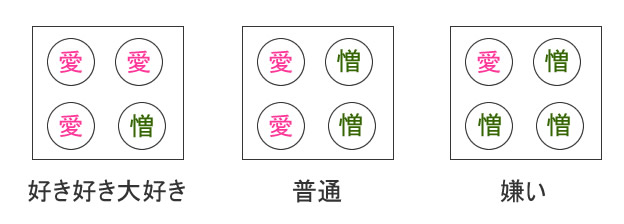
心を原因の箱と考えて、

• “愛”が出たらデートでの良い印象
• “憎”が出たらデートでの悪い印象

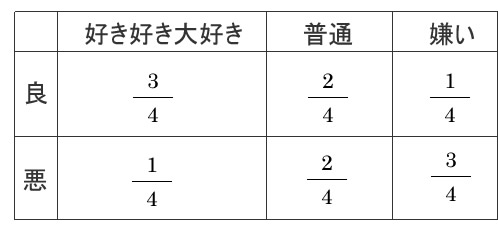
とする。

 

 

事前確率の設定

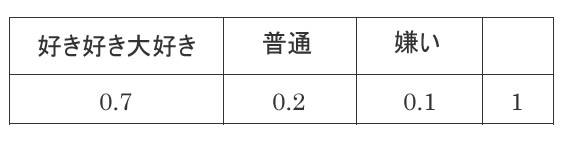
• A子ちゃんのこれまでの彼氏とのデートでの経験、愛されているはずだという信念から「好き好き大好き」を0.7に設定
• A子ちゃんが酔っ払った時に出た方言から都会人の彼氏がひいてしまったかもしれないと考え、「普通」を0.2に設定
• 「嫌い」ならデートだってしないでしょう？その信念から「嫌い」を0.1に設定

 

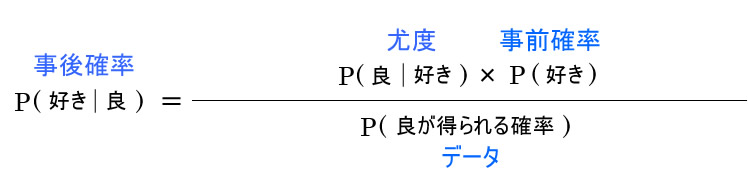
分母の”良”を得る確率を出します。

 

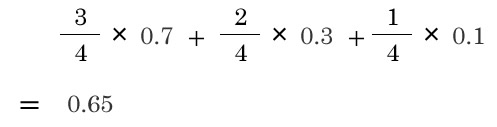
加法定理で分母0.65が出ました。

 

 

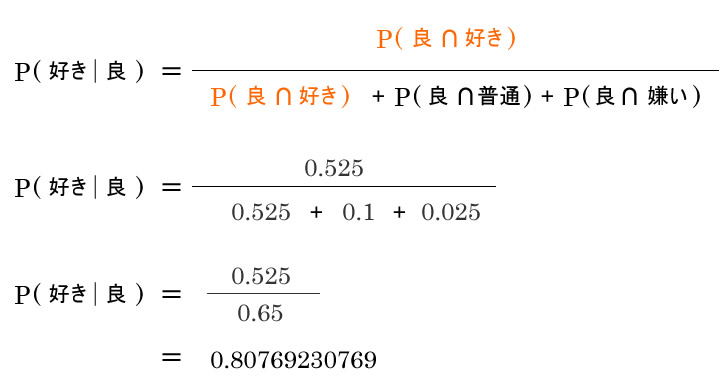
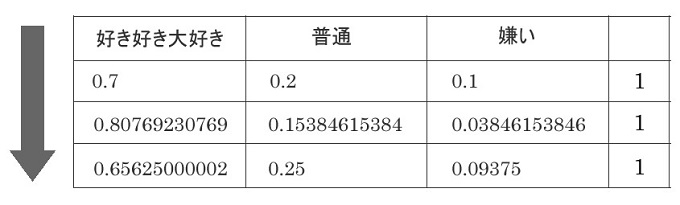
他の事後確率も出して整理します

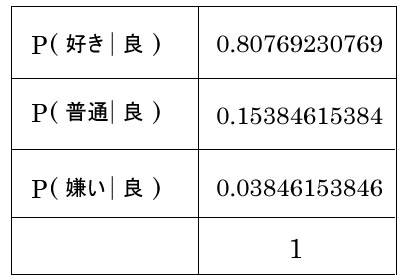
これでそれぞれ出ました。

1回目のデートで”良い”印象は「好き好き大好き」という彼氏さんのA子ちゃんへの想いから生まれた可能性が高いことがわかります。

 

次は2回目のデートで出た”悪い印象”のデータから推定します

 

２回目のデートでの検証では、1回目のデートで得られた事後確率が事前確率になる。

↓ベイズ更新

彼氏さんがA子ちゃんを「好き好き大好き」と想っている確率が0.7から0.8にアップして、「普通」や「嫌い」の確率がダウンしていることがわかりますね！

 

2回目のデートで”悪い印象”というデータが出ました、このデータから彼氏さんはA子ちゃんをどう感じているのでしょうか？

• １回目のデートでの結果で出た事後確率が２回目の事前確率になる
• 尤度は変わらない

 

悪い印象を得た時に「好き好き大好き」である確率を推定します。

 

分母であるP(悪が得られる確率)

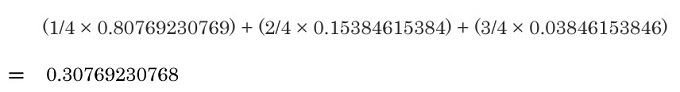
出ましたね。

 

事後確率を整理する

 

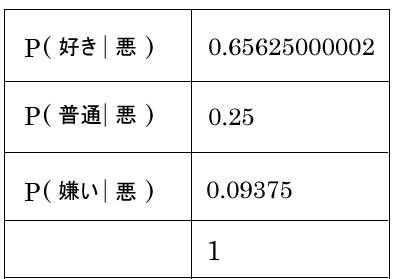
そしてこれは第3回目のデートでの事前確率になります。

このように”良い印象”, “悪い印象”という結果となるデータから、原因となる「好き好き大好き」「普通」「嫌い」の確率を更新することが出来ます。

彼氏さんがA子ちゃんを「好き好き大好き」と想っている確率は0.7から下がってしまいましたが、どんどんデートして精度をあげていきましょ～！

 

 

ナイーブベイズフィルタ

迷惑メールフィルタリング

あるメールに「有効期限」「無料プレゼント」「政治学」のワードが本文に含まれている場合に、このメールが迷惑メールか通常メールか振り分けたい。

 

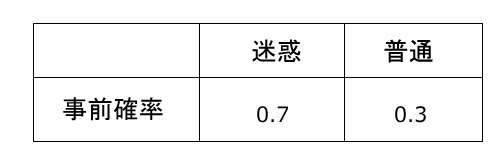
事前確率

世の中に流通するメールの0.7は迷惑メールで、0.3が通常メールであるとして設定

 

尤度

尤度も主観でざっくりと設定

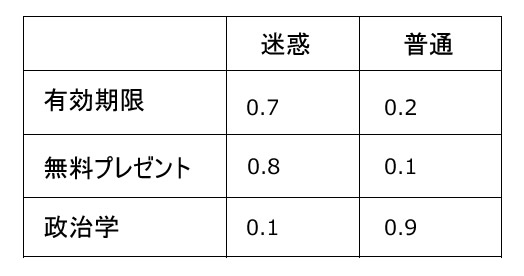
// 尤度は事後確率や事前確率はすべてを足すと1にならなくてはいけないが、「有効期限」など尤度に関しては各項目で迷惑尤度 + 普通尤度でそれぞれ1にならなくて良い。

 

迷惑メールらしさと普通メールらしさの比較なので、分子の大小のみで比べても結果は変わりません。

だから分子のみを比べることで計算を簡略化します。

 

• 「有効期限」「無料プレゼント」「政治学」が含まれるメールが迷惑メールである確率
  0.7 × 0.8 × 0.1 × 0.7 = 0.0392
• 「有効期限」「無料プレゼント」「政治学」が含まれるメールが普通メールである確率
  0.2 × 0.1 × 0.9 × 0.3 = 0.0054

迷惑メールである確率0.0392 ＞ 普通メールである確率0.0054

→迷惑メールである

 

備考

• 単語間の相関関係は実際にはありますが、ナイーブベイズフィルタでは無視して考えます。
• 迷惑メールかどうかの判断は赤玉を取り出した箱の例と変わりません。迷惑メールの箱から赤球を取り出したと考えることが出来ます。

 

 

MAP推定

Maximum a posteriori. 「事後確率が一番大きいものが最もよく発生する」と推定する。

例) 米の生産地

あるお米を食べて”モチモチしている”と感じた時に、「コシヒカリ」, 「あきたこまち」, 「ササニシキ」のどれが最も確率が高いか？

 

尤度

お米の特徴から”モチモチしている”尤もらしさをざっくり設定

// 尤度の合計を1にしていますが、1にする必要はないです。

 

事前確率

生産量からざっくり設定

 

モチモチしていると感じた時に、コシヒカリである確率

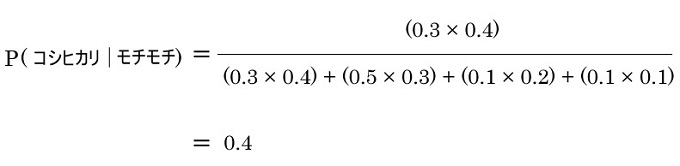
0.4と出ました、他の品種に関してもベイズの展開公式を利用して同様に行います。

MAP推定の考え方として、事後確率が一番高い「あきたこまち」がモチモチしていると感じたお米の品種である確率が高いとされます。

 

 

ベイズ意思決定

雇用統計の発表によって実際の景気と、どの金融商品を選んだら良いかを考えます。

1. 雇用統計の発表によって実際の景気の事後確率を算出
2. 事後確率から金融商品の期待値を算出

 

 

尤度

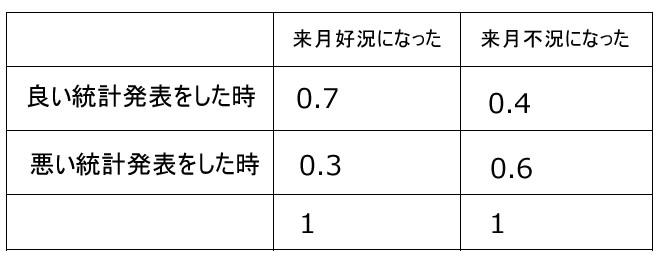
雇用統計の発表によって好況, 不況の尤度を設定

 

事前確率

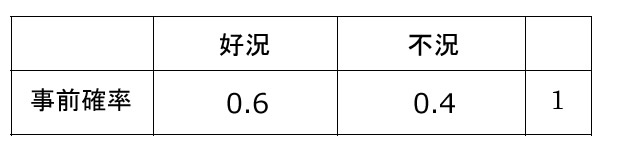
過去10ケ月間の実際の好況、不況の割合から設定

 

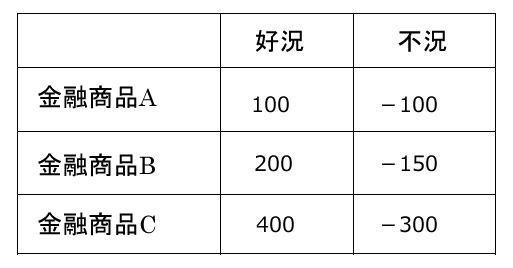
金融商品

 

良い統計が発表された時に好況になる事後確率

 

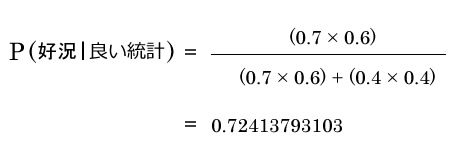
良い統計が発表された時に不況になる事後確率

 

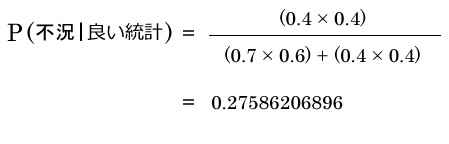
悪い統計が発表された時に好況になる事後確率

 

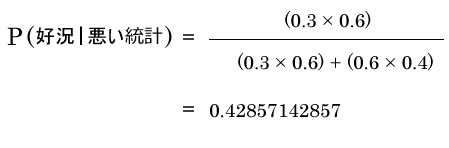
悪い統計が発表された時に不況になる事後確率

 

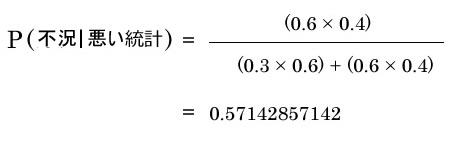
事後確率

 

 

期待値を出す

 

 

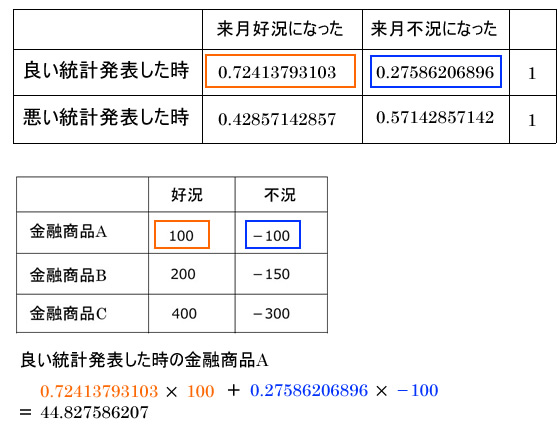
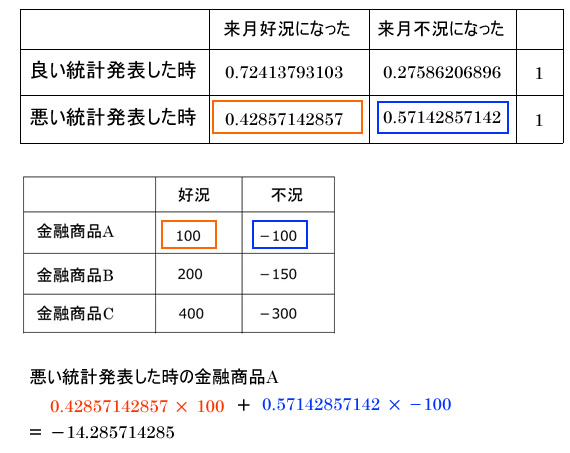
期待値が出る

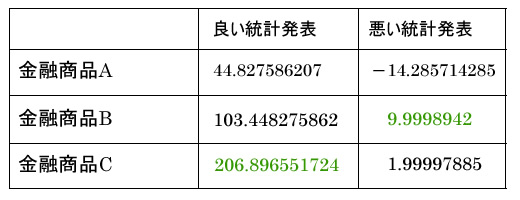
• 良い統計発表の時は金融商品Cを買う
• 悪い統計発表の時は金融商品Bを買う

 

 

ベイジアンネットワーク

ベイジアンネットワークの利点は、判断となる処理の過程が見えること。

機械学習の有力なアルゴリズムとして利用される｢ディープラーニング｣は判断の過程と予測の過程がブラックボックスになる問題があり、判断が間違っていた場合に人間にはAIが下した判断の過程がわからないので修正が難しい。

>写真や画像を無料で保存できるGoogle Photosには機械学習が使われており、類似のコンテンツ認識し、自動でラベル付きで分類してくれます。2015年にこのGoogle Photosが黒人を「ゴリラ」とラベリングしたことが大きなニュースとなりましたが、2年たってどれだけ画像認識技術が進歩したかがチェックされたところ、「Google Photosはゴリラを見えないものとしている」ということがわかりました。

@see Gigazine Googleはゴリラ画像を検索結果からブロックしている

 

 

警報機の例

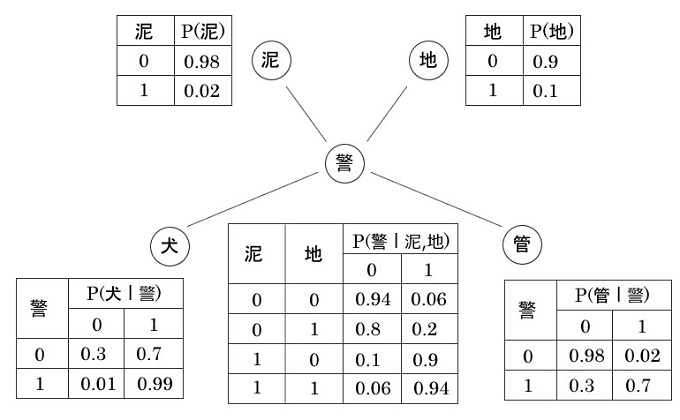
// 確率変数で、0は何も起こらない、1は確率変数が発生することを意味します。

例題

• 振動によって感知する警報機がある、この警報機は泥棒でも地震でも上記の確率でアラートする。
• 警報機がアラートすると犬はわんわん鳴く
• 警報機がアラートすると管理人は警察に通報することになっている
• ただし犬はお腹が減ればわんわん鳴く。
• 管理人は海外ドラマに夢中になると警報機に気付く確率が下がりがちになるようだし、警報機のアラートが鳴った気がして通報してしまうこともあるみたいだ。

 

① 泥棒が入り、警報機がアラートを出して、管理人が通報する確率はいくつか？

通常の確率計算を行います。

• 泥棒が入る確率 P(泥=1) = 0.02
• 地震が起こらない確率 P(地=0) = 0.9
• 泥棒が入った時に警報機がアラート出す確率 P(警=1∣泥=1) = 0.9
• 警報機がアラートを出した時に管理人が通報する確率P(管=1) = 0.7

0.02 × 0.9 × 0.9 × 0.7 = 0.01134

≒1%

 

 

②管理人が通報した時に、実際に泥棒が入っていた確率はいくつか？

ベイズの定理を利用します。

事後確率 P(泥=1∣管=1)を求めるのに必要な確率

1. 事前確率 P(泥=1)
   泥棒が入る確率
2. P(管=1)
   管理人が通報する確率
3. 尤度P(管=1∣泥=1)
   泥棒が入った時に管理人が通報する確率

 

事前確率 P(泥=1) 泥棒が入る確率

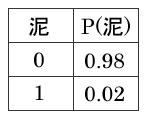
表より0.02

 

P(管=1) 管理人が通報する確率

• 警報機のアラートがない時に管理人が通報する時
  P(管=1∣警=0) × P(警=0)
• 警報機のアラートがあって管理人が通報する時
  P(管=1∣警=1) × P(警=1)

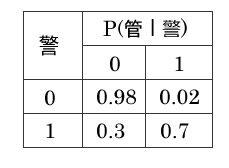
P(管=1) = P(管=1∣警=0) × P(警=0) + P(管=1∣警=1) × P(警=1)

= 0.02 × P(警=0) + 0.7 × P(警=1)  ･･･①

 

P(警=1),P(警=0)の確率がそれぞれ必要

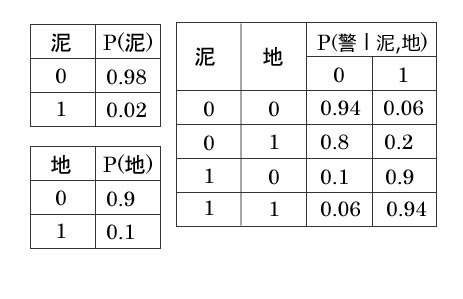
P(警=1)
= P(警察=1∣泥=0,地=0) × P (泥=0) × P(地=0)
+ P(警察=1∣泥=0,地=1) × P (泥=0) × P(地=1)
+ P(警察=1∣泥=1,地=0) × P (泥=1) × P(地=0)
+ P(警察=1∣泥=1,地=1) × P (泥=1) × P(地=1)

= (0.06 × 0.98 × 0.9)
+ (0.2 × 0.98 × 0.1)
+ (0.9 × 0.02 × 0.9)
+ (0.94 × 0.02 × 0.1)

= 0.0906 ･･･②

 

P(警=0)

= 1 − P(警=1)
= 1 − 0.0906
= 0.9094 ･･･③

 

②, ③を①に代入する
0.02 × P(警=0) + 0.7 × P(警=1)  ･･･①

 

(0.02×0.9094)+(0.7 × 0.0906)
= 0.081608

 

 

尤度P(管=1∣泥=1) 泥棒が入って管理人が通報する確率

泥棒が入って管理人が通報する確率
= 泥棒が入ってかつ警報がアラートを出した時に管理人が通報する確率
+ 泥棒が入ってかつ警報がアラート出さなかった時に管理人が通報する確率

 

 

=
{ (0.9 × 0.9) + (0.94 × 0.1) } × 0.7
+ { (0.1 × 0.9) + (0.06 × 0.9) } × 0.02

= 0.6328 + 0.00288
= 0.63568

 

1. 事前確率 P(泥=1) 0.02
   泥棒が入る確率
2. P(管=1) 0.081608
   管理人が通報する確率
3. 尤度P(管=1∣泥=1) 0.63568
   泥棒が入った時に管理人が通報する確率

P(泥=1∣管=1) =0.63568×0.02/0.081608

=0.15578864817
≒15.6%

 

 

ノード

• 原因となるものを親ノード
• 結果となるノードを子ノード

 

マルコフ過程(Marcov Process)

将来の状態(管)は現在の状態(警)からしか依存しないことをマルコフ過程、取りうる状態が有限なものをマルコフ連鎖(Marcov Chain)という。