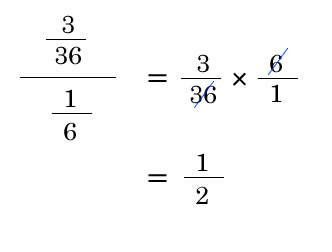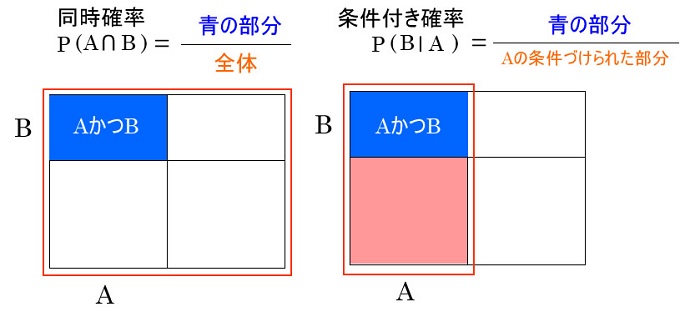
// ジョーカーを抜いたトランプ
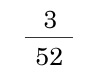
例) 条件付き確率 :ハートであった時に絵柄 P(絵柄∣ハート)
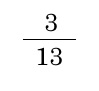
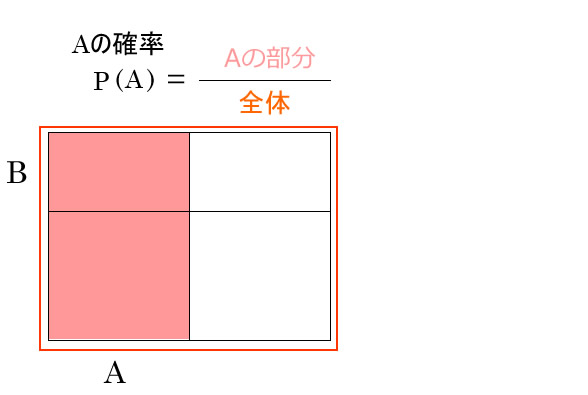
例) ハートの確率 P(ハート)
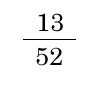
もくじ
乗法定理
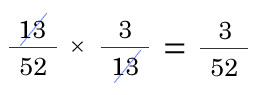
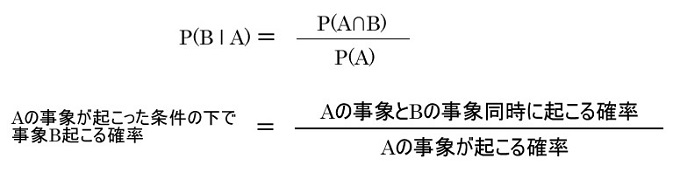
条件付き確率
例 人選び
- 体育が得意なのが男子10人、女子8人
- 英語が得意なのが男子4人、女子6人
女子が選ばれた時に、体育が得意である確率 P(体育∣女子) はいくつか?
速攻計算する場合
体育が得意な女子8人/女子14人
= 8/14
= 4/7
丁寧に計算する場合
P(体育∣女子)
= P(女子体育) / P(女子)
= { P(女子) × P(体育∣女子) } / P(女子)
女子が選ばれた時に、体育が得意である確率
= 女子が選ばれたかつ体育が得意な確率 / 女子が選ばれる確率
= (女子総数14人/男女総数28人 × 体育得意8人/女子総数14人) / 女子総数14人/男女総数28人
= (14/28 × 8/14) / 14/28
= 8/14
= 4/7
例 サイコロ
1回目にサイコロを振った時に4が出た時に、2回目に振ったサイコロとの合計が8以上になる確率はいくつか?
1回目に4が出る確率
= 1/6
1回目に4で、1回目と2回目のサイコロの出目の合計が8以上になる組み合わせ
- (4, 4)
- (4, 5)
- (4, 6)
3通り
2回サイコロを振った時の組み合わせの総数
6通り × 6通り = 36通り
= 3/36
= 1/12
P(合計が8以上∣1回目の出目4)
= 1回目の出目4かつ1回目と2回目の合計が8以上の確率 / 1回目の出目4