コミットのメアドなどを晒したくなかった次第 https://github.com/settings/emails Keep my email addresses private We’ll remove your public profile email and use 11024212+yuukanehiro@users.noreply.github.com when perfor …
GitHubのメールアドレスを匿名設定
Mac Book Pro M2 13インチで外部ディスプレイを2枚にする
個人事業用PCにと、M2 13インチを購入したら外部ディスプレイが1枚しか使えなかった😭 購入したもの MacBook Pro 13 M2 2022 RAM24GB/SSD512GB Anker 564 USB-C ドッキングステーション DisplayLink対応ドッキングステーションを購入 DisplayLinkドライバ導入手順 homebrewインストール Dis …
[Solved]VS Code | Error loading workspace: packages.Load error: err: exit status 1: stderr: go: go.work requires go >= 1.24.2 (running go 1.22.3)
1.22.3から1.24.2にGoをUpdateした後にVS Codeで読み込みエラーが発生 Error loading workspace: packages.Load error: err: exit status 1: stderr: go: go.work requires go >= 1.24.2 (running go 1.22.3) 問題なし VS …
[MySQL] rangeが絡むバッチサイズの計算
range_optimizer_max_mem_sizeを超えた場合のrangeはFull Scanになってしまう。 対策 Full Scanにならないようにバッチサイズを見積もる 前提 MySQL7.0以上 見積もり方 range_optimizer_max_mem_sizeの値を検索する INで指定する要素にかかるサイズは230バイト になるようにBatchサイズを見積もること …
SQL速度改善 EXISTS
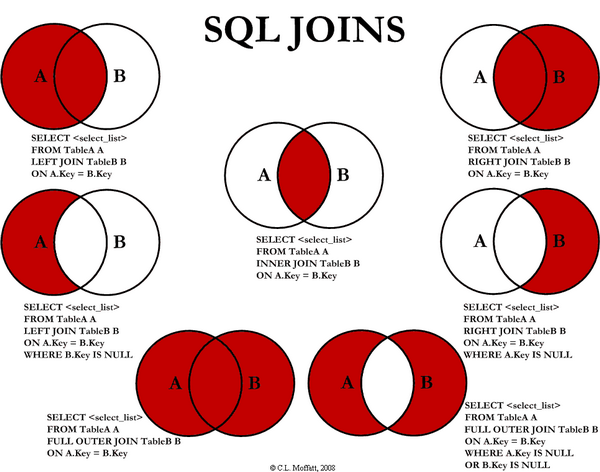
EXISTSはレコード数が増加すると速度が悪化する EXISTSはINNER JOIN NOT EXISTSは副問い合わせ OR EXISTSはUNION ALL 上記に変更できないかを検討する
Golang []byteをio.Readerに変換。io.Readerを[]byteに変換
io.Readerから[]byteに変換 []byteからio.Readerに変換 byte型 符号なしの8bitの値 []byte型 byte型のスライス io.Reader []byteを読み出す為のインターフェイス Readメソッドを持つ
performance_schemaでのロック待ち、スロークエリ分析
引用元 https://zenn.dev/hiro1111/articles/performance_schema ステートメント分析 最もリソースを消費しているSQLステートメントを特定します。以下のクエリは、CPU時間、待機時間、ロック時間、およびIO時間で最もコストが高いステートメントを見つけます。 待機イベント分析 データベースの待機イベントを分析 …
SESのバウンスレート(BounceRate)を下げるハック
SESのBounceRateを下げる為のハック ・正常なアドレスにダミー送信することで全体の正常数をかさましすることで回避する AWS Messaging & Targeting Blog We recommend that you send at least 20 messages to “good addresses” for every one you s …
ドモルガンでSQLリファクタ
NOT (A or B) = (NOT A) and (NOT B) 抽象例 具体例 リファクタ NOT (A and B) = (NOT A) or (NOT B) 抽象例 具体例 リファクタ
Golang Twitter ちょっとしたDBの物語 タロウさんの口座に10万円入っていました。
ちょっとしたDBの物語 タロウさんの口座に10万円入っていました。 A処理:口座引き落とし5万円 B処理:給与振り込み２０万円 AとBはタイミングがかち合いました。 A処理、残高チェック:10万円 B処理、残高チェック:10万円 B処理、10万+20万＝30万で更新 A処理、10万-5万＝5万で更新 最新口座残高は？ — SEライダー (@Sys_Rider) May 13, 202 …
GitHub | git-pr-lease
実行 公式 https://github.com/x-motemen/git-pr-release 弊社ではmakeコマンドを作ってる
Text Blazeとショートカットでレビューコメントのタグ付け
Chrome拡張機能 https://chromewebstore.google.com/detail/text-blaze-templates-and/idgadaccgipmpannjkmfddolnnhmeklj /must 修正必須 /imo 修正任意 個人的な見解。私の意見では /imho 修正任意 私の意見では(でも他の人は違う意見かも) /nits 修正任 …