ベイズの定理(ベイズのていり、英: Bayes’ theorem)とは、条件付き確率に関して成り立つ定理で、トーマス・ベイズによって示された @see Wikipedia ベイズの定理 ベイズが完成させた定理は圧巻のパフォーマンスと世界観で幅広いオーディエンスを歓喜の渦に巻き込んだ。没後250年で死後の念が強まり、今なお彼を信仰する”ベイジアン”によって機械学習 …
ベイズ確率まとめ

var 優技録 = []string{ "Golang", "Vue.js", "AWS", "PHP", "DB", "IaC", "SRE"}

ベイズの定理(ベイズのていり、英: Bayes’ theorem)とは、条件付き確率に関して成り立つ定理で、トーマス・ベイズによって示された @see Wikipedia ベイズの定理 ベイズが完成させた定理は圧巻のパフォーマンスと世界観で幅広いオーディエンスを歓喜の渦に巻き込んだ。没後250年で死後の念が強まり、今なお彼を信仰する”ベイジアン”によって機械学習 …
ルール A, B, Cの扉の先に正解がある まずゲストはA, B, Cのいずれかの扉を選ぶ 正解の扉を知っている司会がはずれの扉を1つ選ぶ ゲストは残った2つの扉のどちらかを改めて選ぶことが出来る権利を与えられる 命題 ゲストは最初の扉の選択を変更した方が良いのか? 司会からはずれの情報を得た前後で確率は変化するのか? どう選ぶのが確率として高いのか ・選んだ扉から変更 …
母数がわかる場合 10枚のくじに当たりが1枚入っていて、3回引いた時に1度は当たる確率 当たる確率 = すべての確率 - 3回ともはずれの確率 1 - (9/10 × 8/9 × 7/8) = 3/10 = 0.3 上記の条件で9回引いた場合に1度は当たる確率 1 - (9/10 × 8/9 × 7/ …
順列と組み合わせの違い 5人の中から2人並べる・・・順列 = 順番を気にする組み合わせ、名前をつけて区別できる組み合わせ。 5人の中から2人選ぶ・・・組み合わせ = 順番を気にしない組み合わせ 順列 順番を気にする組み合わせ nPr 要素が同じ場合 nPn = n! 4人が4つの椅子に座 …
重複順列 n個の中からr個選ぶ順列は、nPr です。重複順列は同じものを『重複を許して』並べて良い組み合わせです。 n個の箱にr個の種類のボールを何度でも入れて良いと考えます。 A, B, Cの文字を重複を許して、2つに並び変える組み合わせ AA, AB, AC BA, BB, BC CA, CB, CC 2つの箱に3つのボールを重複を許して入れていくと考 …
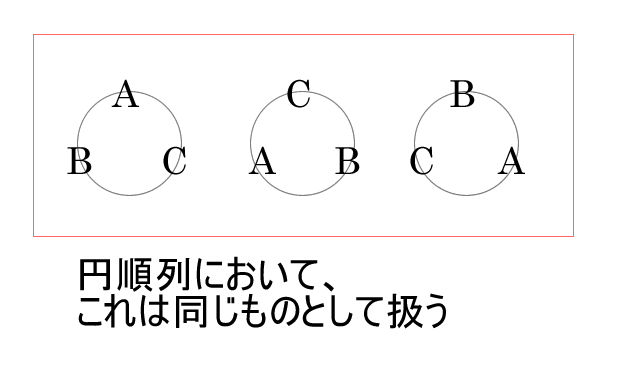
円順列 (n - 1)! ex) A, B, C, D, Eさんの5人を円卓で並ばせる組み合わせ (5 - 1)! = 4! = 4 × 3 × 2 × 1 = 24通り 一人をピンで固定して、残りの人間が入れ替わる順列として考えます。 ex) 男5人, 女5人の男女10人が隣合う並び方、同性が隣合わあない並び方 …
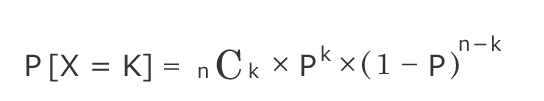
二項分布 ex) 表の確率が20%, 裏が80%の確率で出る特殊なコインを5枚投げて、表が3枚出る確率 ex) 赤玉1つ、青玉2つ、白玉3つが入っている抽選機があり、一度抽選を引くたびに玉は戻すとします。3回抽選を行った時に赤玉が2つ出る確率 多項分布 ex) 赤玉1つ、青玉2つ、白玉3つが入っている抽選機があり、 …
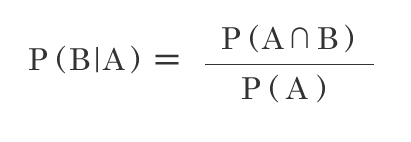
条件付き確率 確率P(A)が起こるとした時の、確率P(B)が起こる確率を表します。 ex) サイコロを振った時に奇数だった時に、5以上である確率 ベイズの定理 条件付き確率を変形させるとベイズの定理を導出出来ます。 ベイズの定理導出 ① ② ③ ①を変形して③になる ③を②に代入します。 ベイズの定理になります。 …
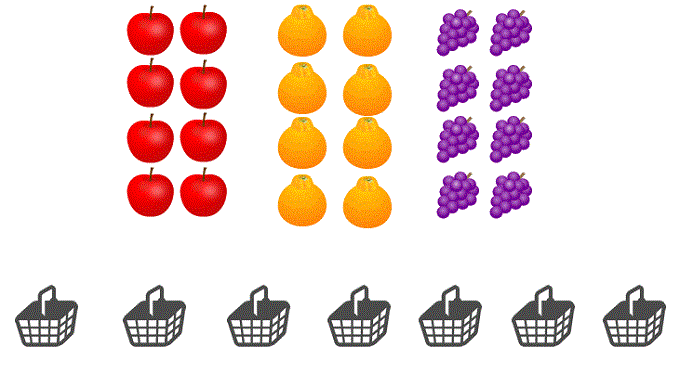
r種類のものからn個選ぶ時の考え方 0個の種類があって良い時 n個+2個の箱にr-1個の棒を入れる組み合わせ 0個の種類がダメな時 n – 1個の箱にr-1個棒を入れる組み合わせ 例) 「りんご」,「でこぽん」,「ぶどう」の3種類のフルーツから7つ選ぶ組み合わせ 上記について考えます。 & …
期待値は確率×確率変数の総和 サイコロを1回振った時の期待値 確率変数 1 2 3 4 5 6 確率 1/6 1/6 1/6 1/6 1/6 1/6 1×1/6 + 2×1/6 + 3×1/6 + 4×1/6 + 5×1/6 + 6×1/6 =1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 3.5 10万円が1本、1万 …

データの密度 平均値と標準偏差を使ってデータの密度を簡単に見ることが出来ます。 平均が0の時の標準偏差は0, また平均値の時のデータは基準値は0、偏差値は50 -1 ×標準偏差 ~ 平均値 ~ 標準偏差× +1 この区間にデータが68.3%含まれている 偏差値で言うと、偏差値40~60 -2 ×標準偏差 ~ 平均値 ~ 標準偏差 …