もくじ
ルール
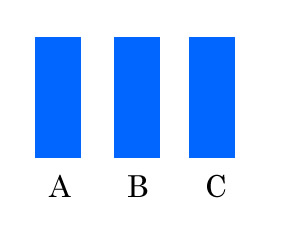
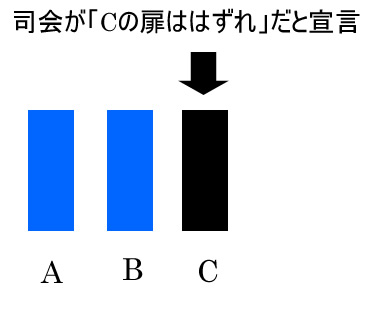
- A, B, Cの扉の先に正解がある
- まずゲストはA, B, Cのいずれかの扉を選ぶ
- 正解の扉を知っている司会がはずれの扉を1つ選ぶ
- ゲストは残った2つの扉のどちらかを改めて選ぶことが出来る権利を与えられる
命題
- ゲストは最初の扉の選択を変更した方が良いのか?
- 司会からはずれの情報を得た前後で確率は変化するのか?
- どう選ぶのが確率として高いのか
・選んだ扉から変更した方が確率として有利なのか
・それとも選択を変えても変えなくても確率は変わらないのか
確率
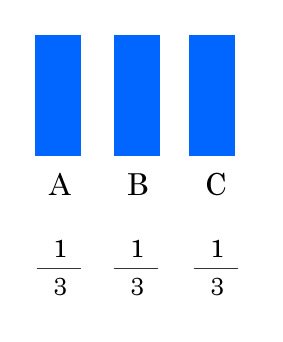
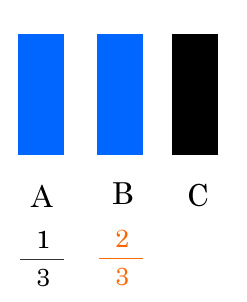
A, B, Cそれぞれ1/3
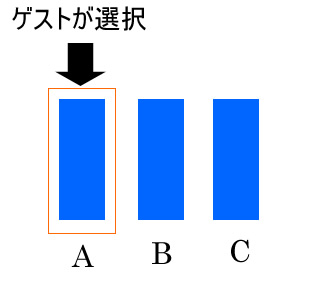
ゲストはAがあたりの扉であると選んだ
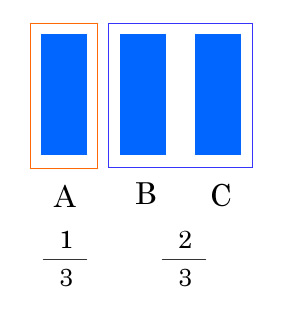
- Aが正解の確率 = 1/3
- BまたはCが正解の確率 = 1/3 + 1/3 = 2/3
// 加法定理
残りはAか、Bの扉になる、
ゲストは扉の選択を変更する権利が与えられる
AからBに変更した方が良いのか、それともAを選択したままにするか?
答え
変更してBを選んだほうが確率が高い
Bに変更するとあたる確率が2倍高くなる
乗法定理
![]()
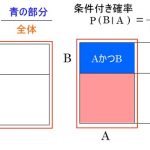
A ∩ B= P(A) × P(B|A)
- ジョーカーを除いたトランプから1枚引いた時に、ダイヤでなおかつ絵柄である確率
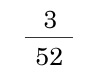
ダイヤでなおかつ絵柄であるカードは52枚の内3枚です。
- ジョーカーを除いたトランプから1枚引いた時に、ダイヤである確率
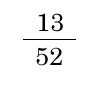
- ジョーカーを除いたトランプから1枚引いた時に、ダイヤであった時に絵柄である確率
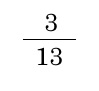
- ジョーカーを除いたトランプから1枚引いた時に、ダイヤでなおかつ絵柄である確率 = ダイヤであった時の確率 × ダイヤであった時に絵柄であった時の確率
![]()
A ∩ B= P(A) × P(B|A)
つまり、
ダイヤ ∩ 絵柄= P(ダイヤ) × P(絵柄|ダイヤ)
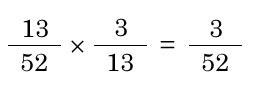
ベイズの定理による考え方

- 最初の状況ではゲストはどれを選んでも1/3になります。
- ゲストはAを選びます
- ここから正解を知っている司会者がはずれを選ぶことで確率が変わります
ベイズの定理の利用
乗法定理をひっくり返してイコールとして等式を作って、変形することで導出
AなおかつBが起こる確率
- = Aが起こった時にBが起こる確率 × Aが起こる確率
- = Bが起こった時にAが起こる確率 × Bが起こる確率
ひっくり返しても当然同じ確率
ベイズの定理
- D: データ
- H: 仮定

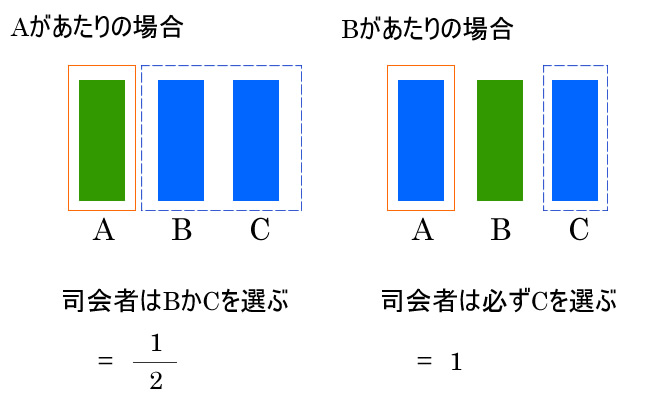
仮定. 扉Aがあたりの場合
司会が扉Cを選んだ時にAが当たりの確率
= 扉Aがあたりの時にドアCが司会者に選ばれる確率 × Aが当たりの確率 / 司会が扉Cを選ぶ確率
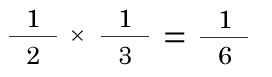
// 分母は共通なので分子のみで比べる
仮定. Bがあたりの場合
司会が扉Cを選んだ時にBが当たりの確率
= 扉Bがあたりの時にCが司会者に選ばれる確率 × Bが当たりの確率 / 司会が扉Cを選ぶ確率
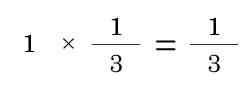
// 分母は共通なので分子のみで比べる
結論
- 司会の情報を得た後で、Aから変更しBを選んだほうが2倍有利になる
// 意思決定の理論 = 情報を得て次にどのように行動するのが最適かを決める理論 - データを得る前後で確率が移り変わる
@see ベイズ統計超入門









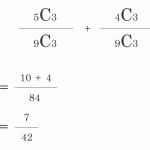
モンティホール問題をベイズの定理で考えれば、司会が扉BかCを選んだ時にAが当たりの確率は1/3で、Bが当たりの確率も1/3、Cが当たりの確率も1/3で、Aが当たりの確率は変化しない。
ご指摘有難う御座います!
お優しいですね、
数学は手習いといったものですので大変助かります。
私生活が立て込んでおりましてすぐに内容を修正することが難しいですが、
タイミングを見て改めて見直させて頂きます。