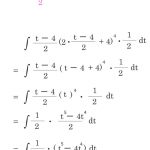Python 偏微分で大満足カレーを作る Matplotlib

寄稿しました。

 

 

 

大満足カレー物語

いつでも美味しく食べられる国民食”ドンカレー”の成功で大富豪と知られるシファーナさんが街で小さなインドカレー屋を営んでいた時のお話。

新製品の開発を考えた結果、カレーのとろみ度とスパイス量が満足度に直結するのではないかとシファーナさんは考えました。そこでカレーのとろみ度X、スパイス量Yをそれぞれ僅かに変化させたカレーでモニターアンケートを取ることで満足度Zとした調査を行った結果、

散布図から下の関数が出来ちゃいました、とさ！

Z = -5x^2 + 4xy -2y^2 +6x +2y +1

// 関数の求め方は最小二乗法

@see

• 優技録 偏微分で最小二乗法 単回帰分析
• 優技録 Excelで単回帰分析

満足度Zが最大になる、とろみ度X、スパイス量Yを求めて大満足カレーを作りたいのです。

 

XとYで微分する

• xで偏微分: -10*x + 4*y + 6 = 0
• yで偏微分: 4*x – 4*y + 2　= 0

これを連立してとろみX, スパイス量Yを出すのですが、計算とか難しい・・・！

偏微分とか面倒クサイ。

難しいことはコンピュータさんに任せましょ～！

 

まず作図してみる

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

def targetfunc(x, y):
    return -5*x**2 + 4*x*y -2*y**2 +6*x +2*y +1

X, Y = np.meshgrid(np.arange(-5., 5., 0.5),
                   np.arange(-5., 5., 0.5))
Z = targetfunc(X, Y)


fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("f(x, y)")

plt.show()

 

大満足カレーグラフの出力

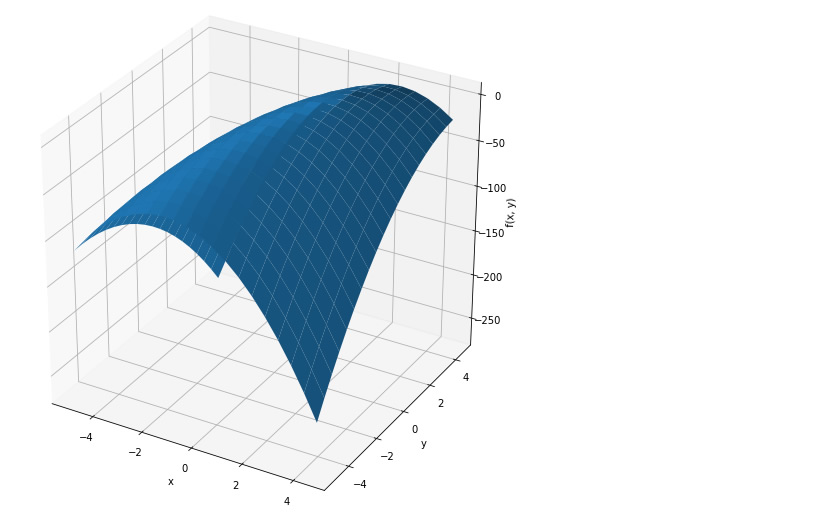
この頂点が大満足ポイント！

 

 

SympyとNumpyで偏微分+連立しちゃおう！

import sympy as sym
sym.init_printing()
(x, y) = sym.symbols("x, y")


targetFunc = -5*x**2 + 4*x*y -2*y**2 +6*x +2*y +1

def AnalyzeCurry(Z):
    dx = sym.diff(Z, x)             # xで偏微分
    dy = sym.diff(Z, y)             # yで偏微分
    s = sym.solve([dx, dy], [x, y]) # dx=0, dy=0で連立方程式
    return dx, dy, s


def main():
    dx, dy, s = AnalyzeCurry(targetFunc)
    print("xで偏微分:", dx)
    print("yで偏微分:", dy)
    print("解：", s)
 
if __name__ == '__main__':
    main()

 

xで偏微分: -10*x + 4*y + 6
yで偏微分: 4*x - 4*y + 2
解： {x: 4/3, y: 11/6}

 

じゃかじゃん！でました。

とろみ度Xは4/3, スパイス量Yは11/6で大満足カレーが完成ですね～！

 

お疲れ様です。