積の法則 独立 = お互いに影響し合わない確率(積) AとBが同時に連続して起こる確率は、 Aが起こる確率とBが起こる確率を掛けます(積) ex)案件Aは90%で成功する、案件Bは70%で成功する。 A, B両方の案件が成功する確率は? 0.9 × 0.7 = 0.63 = 63% ex …
確率 積の法則(独立), 和の法則(排反)
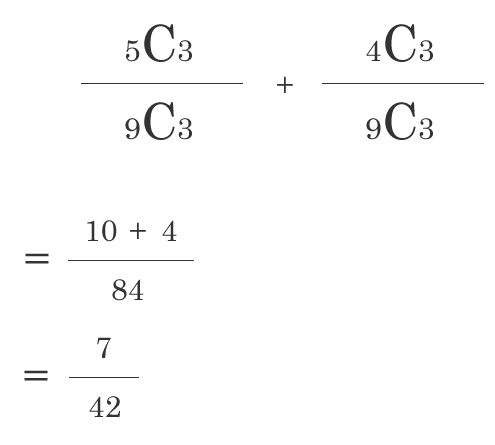
var 優技録 = []string{ "Golang", "Vue.js", "AWS", "PHP", "DB", "IaC", "SRE"}
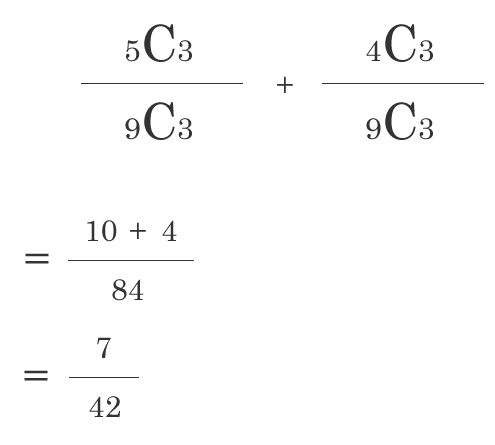
積の法則 独立 = お互いに影響し合わない確率(積) AとBが同時に連続して起こる確率は、 Aが起こる確率とBが起こる確率を掛けます(積) ex)案件Aは90%で成功する、案件Bは70%で成功する。 A, B両方の案件が成功する確率は? 0.9 × 0.7 = 0.63 = 63% ex …
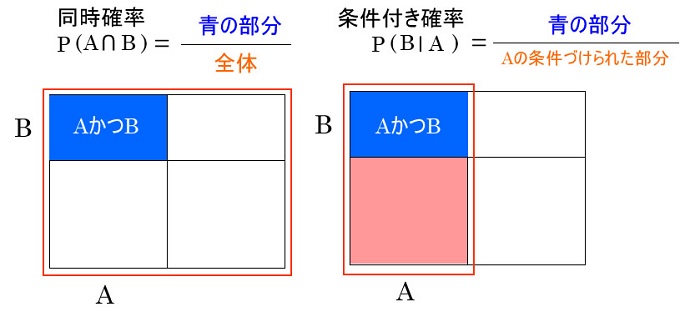
// ジョーカーを抜いたトランプ 例) 同時確率 :ハートかつ絵柄 P(ハート絵柄) 例) 条件付き確率 :ハートであった時に絵柄 P(絵柄∣ハート) 例) ハートの確率 P(ハート) 乗法定理 P(ハート) × P(絵柄∣ハート) = P(ハート絵柄) 条件付き確率 例 人選び 体育が …
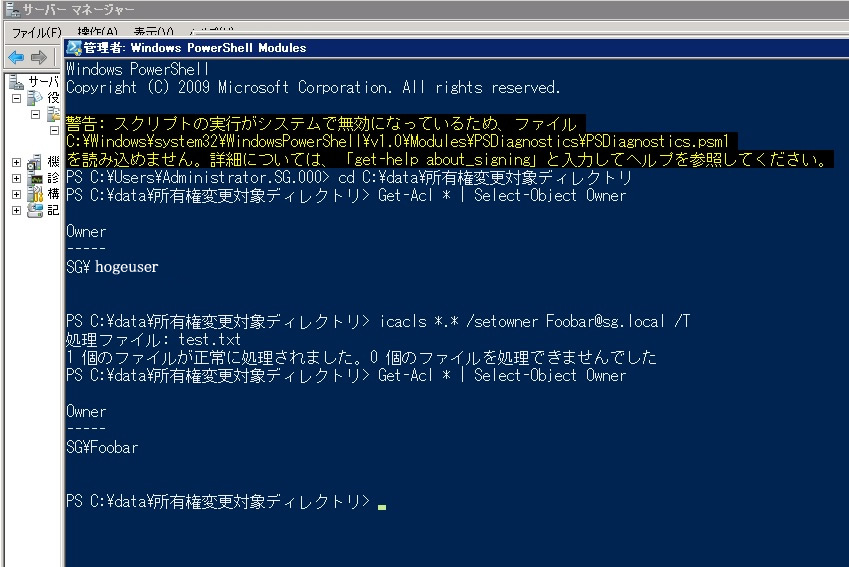
Windowsサーバ 共有ファイルの所有権設定を一括で変更する PowerShell icacls https://sys-guard.com/post-12687/ 所属会社のチップスで書いたものです。 icaclsコマンドを使おう! 所有権変更対象ディレクトリまで移動します。 cd C:\data\所有権変更対象ディレクトリ 所有権を確認します。 PS C:\dat …
OutlookなどMicrosoft関連のソフトウェアは日本語文字コードをSjisで扱うので、Linux上で文字化けしていたりします。その場合にコマンドで文字化けしたディレクトリやファイルを指定しようとしてエラーが発生します。 そんな時はinodeを指定するのが簡単です。 iオプションでinodeを表示させる # ls -liaht 22288799 drwx—— 5 pop …
旅人算 乙姫と彦星は3000m離れています、乙姫は毎分10m、彦星は毎分90mのスピードで接近し合います。何分後に二人は出会えるか? 3000 = 10x + 90x 3000 = 100x x = 30 答え. 30分後 流水算① 4km/hで流れている川があります、 静水時に20km/hで進む船は …
とりあえず無効にする。 # getenforce Enforcing # vi /etc/sysconfig/selinux SELINUX=enforcing ↓変更 #SELINUX=enforcing SELINUX=disabled # reboot now ローカルなのでこっちも無効にする。 # systemctl stop firewalld Remi レポジトリのインストール # y …
Plesk Onyxの各ユーザの送信済メールディレクトリ「.Sent」, 「.Sent Items」を検索しました # find /var/qmail/mailnames/example.net/ -iname .Sent* /var/qmail/mailnames/example.net/hogeTarou/Maildir/.Sent /var/qmail/mailnames/ex …
ある日ドメインが作成出来なくなったりした。 開発元のOrdin様にも見て貰いrpmが破損していることを確認。 以下はrpmリビルドによる復旧作業内容 # rpm -qa | grep php rpmdb: Thread/process 8480/140060972062688 failed: Thread died in Berkeley DB library error: db3 …
A = Bの証明 Aの計算結果、Bの計算結果が等しくなった A - B = 0になった A = C, B = Cになった 背理法 背理法でA = Bを証明する場合 A ≠ Bを仮定する 本当に証明したいものの否定系を仮定します。 A ≠ Bの仮定に矛盾を見つける A ≠ Bが矛盾して成り立たなくなる 背理法によりA = Bが証明された! A …
Table 3. ドメイン コントローラの最少数 ドメインごとのユーザー数 ドメインごとの最小のドメイン コントローラ数 1–499 One – Single Processor 500–999 One – Dual Processor 1,000–2,999 Two – Dual Processor 3,000–10,000 Two – Quad Processor …
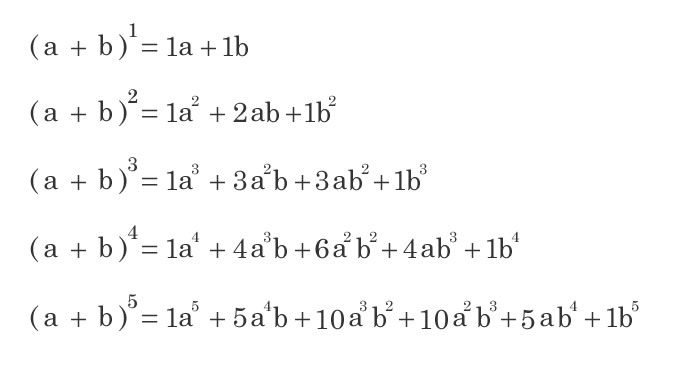
上記の暗記はしなくて大丈夫 (a+b)^2 = (a + b)(a + b)について考える と考える。 パターン bの目線で係数について考える // aの目線で考えても同じようになります。 (a+b)^3 = (a + b)(a + b)(a + b)について考える パスカ …
会社の記事に投稿したもの。基本的に下記の値で安定するけれど、きちんと時系列を把握しておいた方が良い。 https://sys-guard.com/post-12263/ スレーブからマスターへ接続するSQL文 MySQLのレプリケーションというと下記のようにスレーブからマスターに接続をかけます。 mysql> CHANGE MASTER TO MASTER_HOS …