最短経路 順列
カテゴリー: 数学
接弦定理 証明
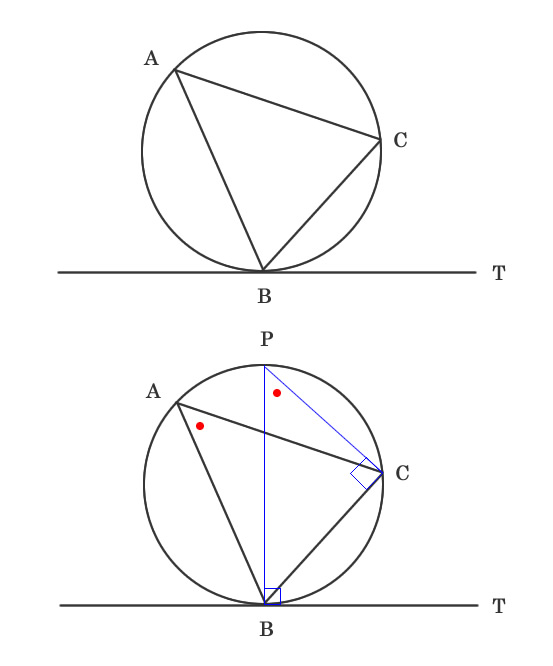
接線Tに対して垂直である円の直径Pの補助線を引くと、 ２つの図のようになる。 円周角の定理から ∠CPB = ∠CAB ・・・① ∠CPB + ∠PBC = 90° ∠PBC = 90° － ∠CPB ･･･② ∠CBT = 90° － ∠PBC ・・・③ ②と③より、 ∠CBT = 90° －(90° － ∠CPB) ∠CB …
三角関数の微分積分の関係
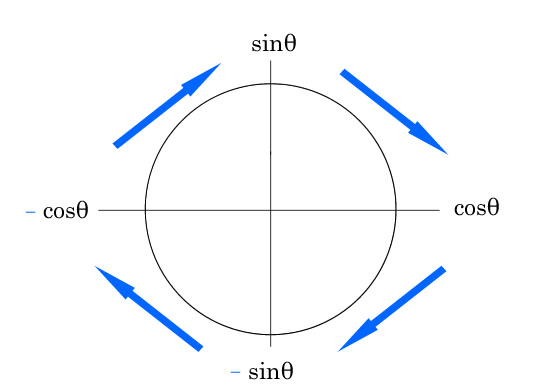
微分 積分 下書き中
命題
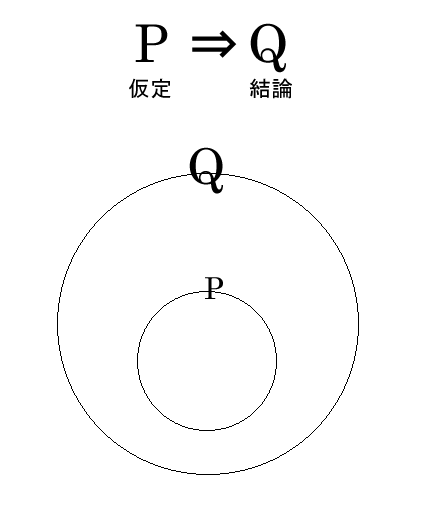
否定 ドモルガンの法則 図 命題において、 対偶同士の真偽値は等しくなります。 exp) 命題 P ⇒ Q 人間であるなら動物である = 真 逆 Q ⇒ P 動物であるなら人間である = 偽(反例 動物=ねこの時、人間ではない) 裏 人間ではないなら動物では …
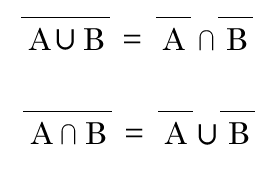
ドモルガンの法則
ドモルガンの法則
マイナスの掛け算の説明
条件 現在地点を0km地点として、 右方向への地点を+方向とする 右方向に時速5Km/hで歩く人の3時間後にいる地点は15Km 距離/速さ・時間 5Km/h × 3h = 15Km 右方向に時速5Km/hで歩く人の3時間前にいた地点 現在いる地点が0km地点とすると-15Km地点にいたことになる 5Km/h × -3h = -1 …
ユークリッドの互除法
550と150の最大公約数 550 = 150 × 3 + 100 150 = 100 × 1 + 50 100 = 50 × 2 + 0 550と150の最大公約数は50 550と150の最小公倍数 50a = 550 × 150 50a = 82500 a = 1650 550と150の最小公倍数は1650 & …
逆関数
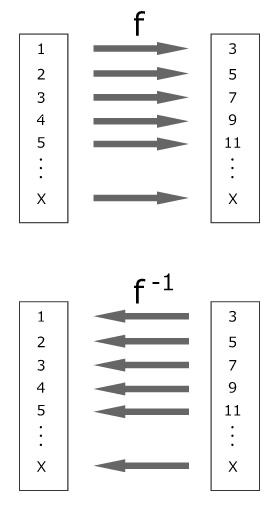
逆関数 関数A Xに1を入れたら、3を返す Xに2を入れたら、5を返す 関数B Xに3を入れたら、1を返す Xに5を入れたら、2を返す この規則性が続くときに関数Aと関数Bは逆関数の関係にあります シンプルな逆関数の例 逆関数の求め方 指数と対数の逆数
偶関数と奇関数の性質と定積分
平行線と線分の比
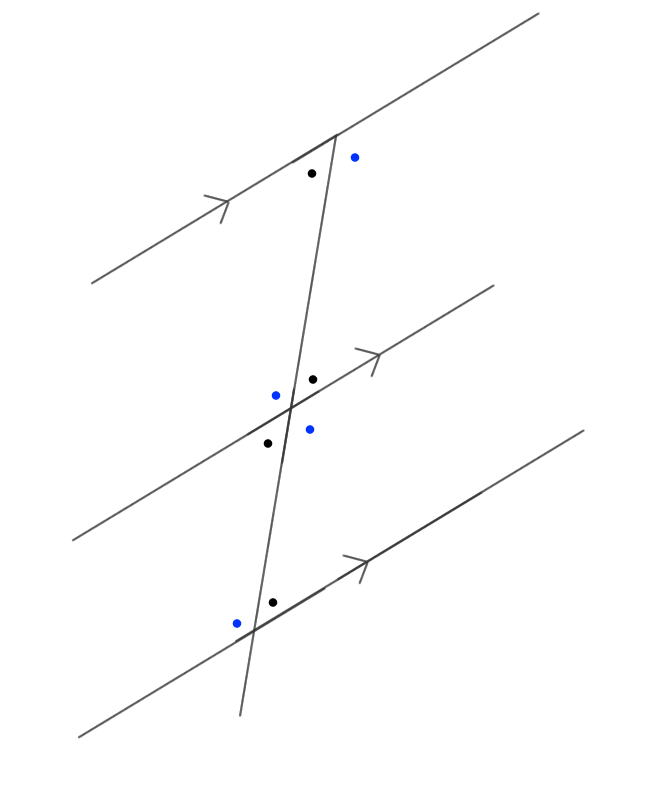
同位角、対項角、錯覚が等しくなる。 線分の比が等しくなる 線分の比が等しくなる、三角形のパターン
角の二等分線定理 証明
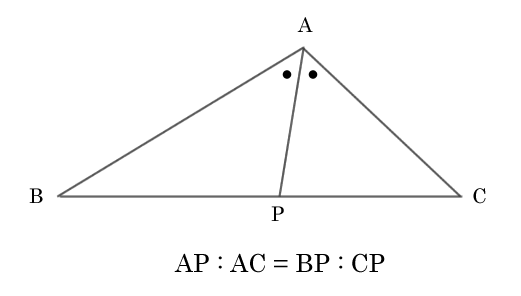
証明 ABに対する線分と平行なる線分ECを作図し、 APを延長させてあげることで、 対抗角と錯覚を利用して△AECは二等辺三角形であるので 相似条件を満たすことで対応する辺の比が等しくなることを証明できます。
三角形の相似, 合同条件
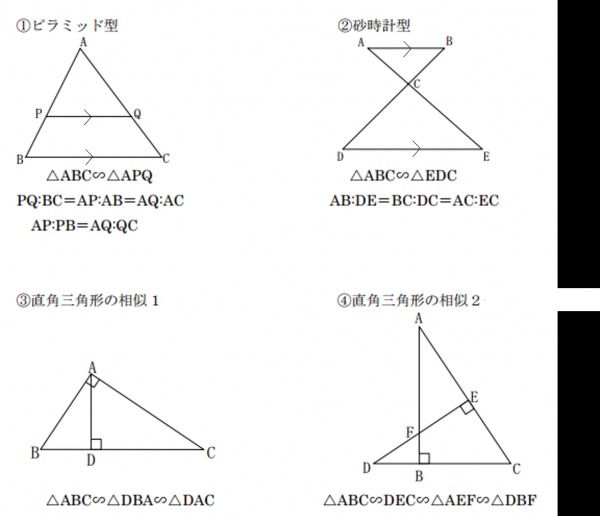
合同条件 3辺の長さが等しい 2辺の長さとその間の角度が等しい １辺とその両端の角度が等しい 合同だとわかると 同じ三角形であるのですべてが等しい 相似条件 3辺の比が等しい 2辺の比とその間の角度が等しい 2組の角度が等しい 相似だとわかると 対応する線分の比が等しい 対応の角度がそれぞれ等しい 1組の辺の比と、もう1組の辺の …