m:nに内分する点の公式 証明 線分ABをm:nに内分する点Pの点を求めます。 m:nに外分する点の公式 証明
線分を内分, 外分する点の公式 証明
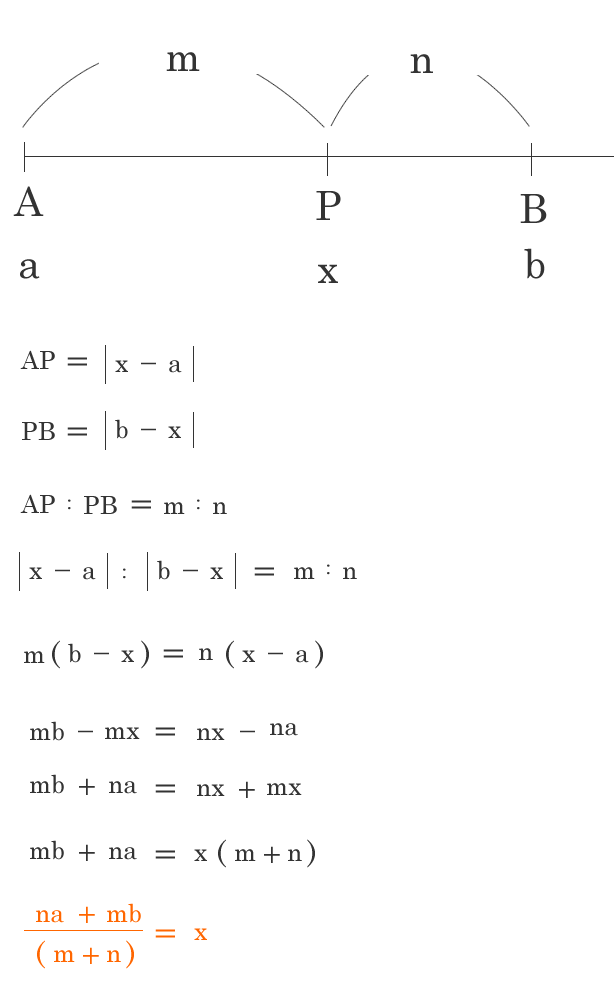
var 優技録 = []string{ "Golang", "Vue.js", "AWS", "PHP", "DB", "IaC", "SRE"}
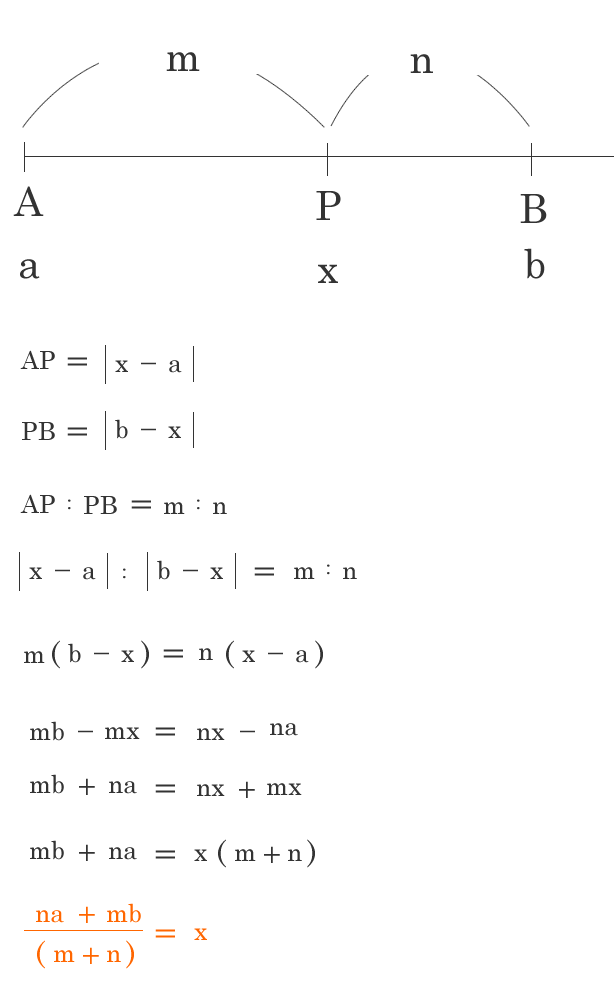
m:nに内分する点の公式 証明 線分ABをm:nに内分する点Pの点を求めます。 m:nに外分する点の公式 証明
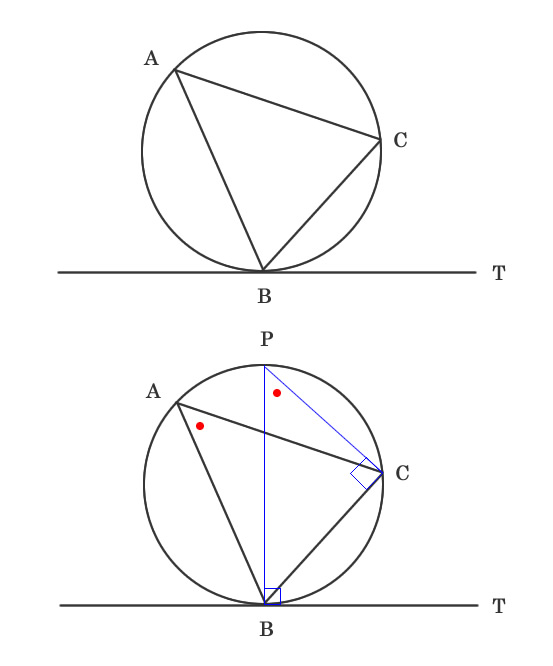
接線Tに対して垂直である円の直径Pの補助線を引くと、 2つの図のようになる。 円周角の定理から ∠CPB = ∠CAB ・・・① ∠CPB + ∠PBC = 90° ∠PBC = 90° - ∠CPB ・・・② ∠CBT = 90° - ∠PBC ・・・③ ②と③より、 ∠CBT = 90° -(90° - ∠CPB) ∠CB …
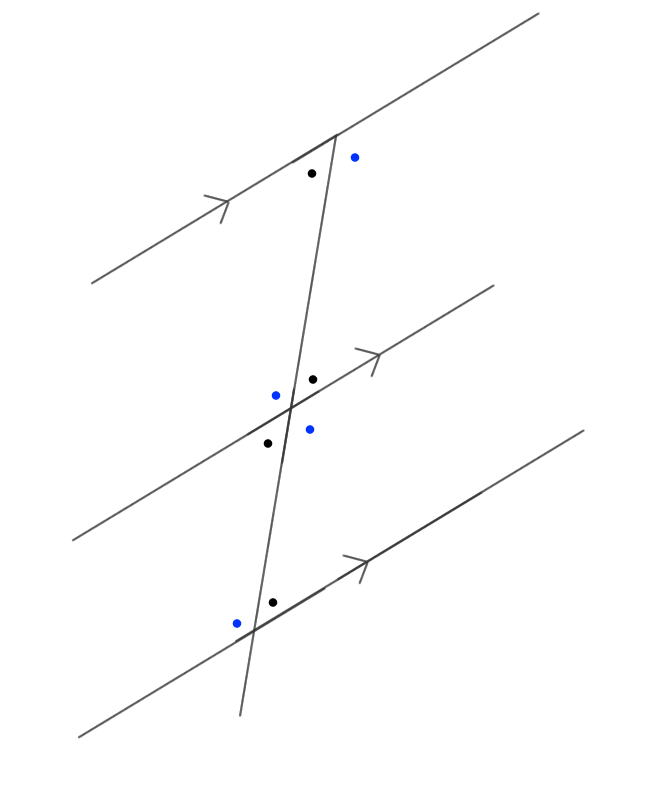
同位角、対項角、錯覚が等しくなる。 線分の比が等しくなる 線分の比が等しくなる、三角形のパターン
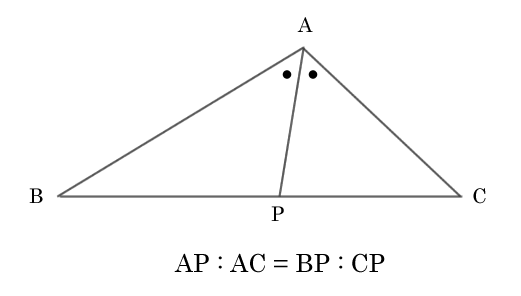
証明 ABに対する線分と平行なる線分ECを作図し、 APを延長させてあげることで、 対抗角と錯覚を利用して△AECは二等辺三角形であるので 相似条件を満たすことで対応する辺の比が等しくなることを証明できます。
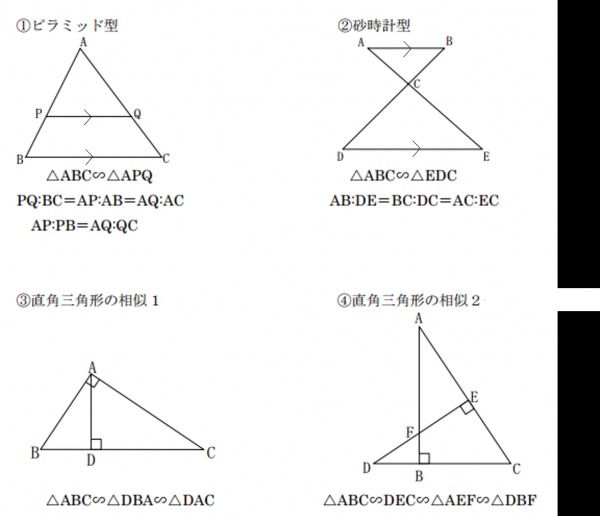
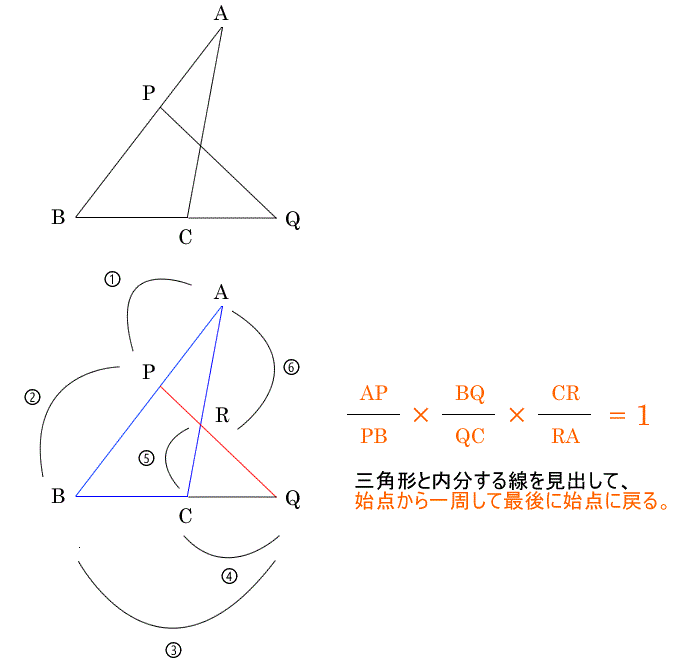
合同条件 3辺の長さが等しい 2辺の長さとその間の角度が等しい 1辺とその両端の角度が等しい 合同だとわかると 同じ三角形であるのですべてが等しい 相似条件 3辺の比が等しい 2辺の比とその間の角度が等しい 2組の角度が等しい 相似だとわかると 対応する線分の比が等しい 対応の角度がそれぞれ等しい 1組の辺の比と、もう1組の辺の …
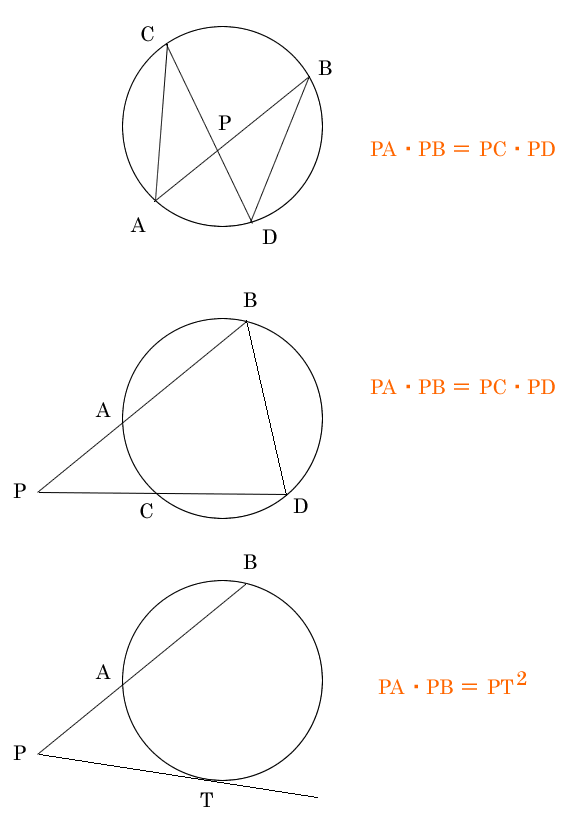
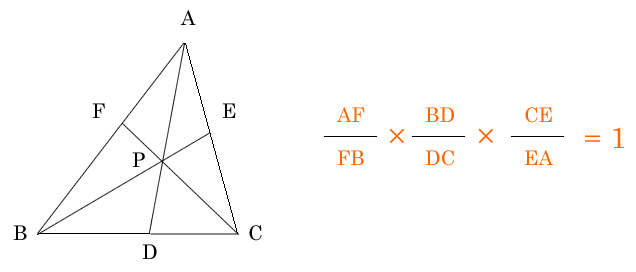
@see https://www.juku.st/info/entry/124
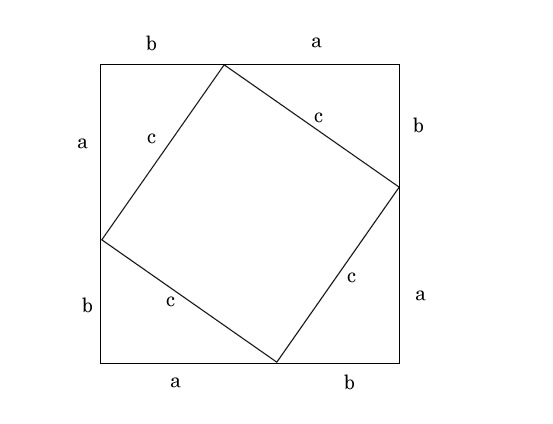
ダヴィンチ版 エレガント